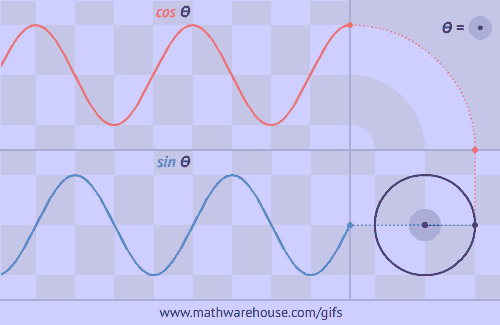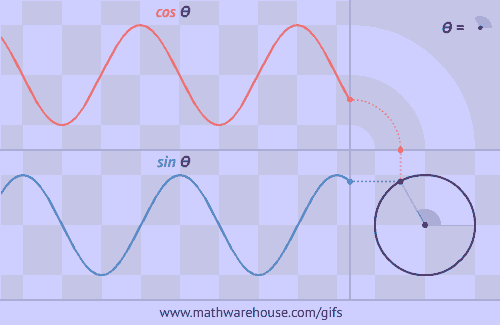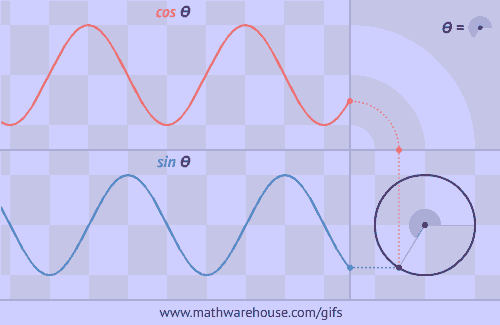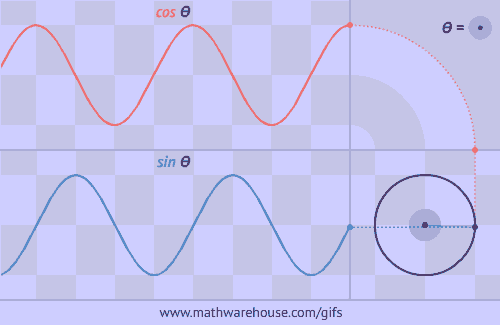
This triangle is impossible.

If the distance between B and C is 0, B and C are the same points. If that is the case, the distances between A and B and A and C must be the same.

However, i ≠ 1.

If you want it to be real (hehe) the triangle should be like this:

    C
    | \
|i| |  \ 0
    |   \
    A---B
     |1|

Drawing that on mobile was a pain.

As the other guy said, you cannot have imaginary distances.

Also, you can only use Pythagoras with triangles that have a 90° angle. Nothing in the meme says that there's a 90° angle. As I see it, there are only 0° and 180° angles.

Goodbye, I have to attend other memes to ruin.

1 • 1 + i • i = 1 + (-1) = 0 = 0 • 0

Pythagoras holds, provided there's a 90° angle at A.

You didn’t really expect an imaginary triangle to behave like a real one, did you?

I get it, it's projected on a comlplex sphere. B and C are the same point

C and B have a wormhole between them

In the complex plane each of these vectors have magnitude 1 and the distance between them is square root of two as you would expect. In the real plane the imaginary part has a magnitude of zero and this is not a triangle but a line. No laws are broken here.

i = 1 is the only logical choice

I kept seeing this pop up recently, and I finally understand it: it's an introductory problem in Lorentzian general relativity.

AB is a space-like line, while AC is a time-like line. Typically, we would write AC as having distance of 1, but with a metric such that squaring it would produce a negative result. However it's similar to multiplying i to the value.

BC has a distance of 0, but a better way of naming this line would be that it has a null interval, meaning that light would travel following this line and experience no distance nor time going by.

I'm sure PBS Spacetime would explain all of this better than me. I just woke up and can't bother searching for the correct words on my phone.

It gets worse once you start doing trig on it

Maybe the problem is constructing a metric that makes this diagram true. Something like d(x,y) = | |x| - |y| | might work but I'm too lazy to check triangle inequality.

Wish me luck for I'm doing trig test with radians (2 pi rad = 360 ?)

funny Interpretation: in the complex plane, the imaginary axis is orthogonal to the real axis. so instead of the edge marked with i (AC), imagine an edge of length 1 orthogonal to that edge. It would be identical to AB, so ~~AC~~ CB is 0.

You can make something like this properly by defining a different metric. For example with metric dl^2^ = dx^2^ - dy^2^ the vector (1, 1) has length 0, so you can make a "triangle" with sides of lengths 1, -1 and 0.

I feel violated trying to read that in my brain.